「Python数据分析系列」10.使用数据

来源 |  Data Science from Scratch， Second Edition

作者 | Joel Grus

译者 | cloverErna

校对 | gongyouliu

编辑 | auroral-L

数据工作既是艺术又是科学。前面我们讨论的大多是数据的科学的一面，这一章我们来探究其艺术的一面。

10.1  探索你的数据

当确定了需要研究的问题，并已获取了一些数据时，你摩拳擦掌地恨不得马上建模求解。但是，你需要克制一下。首先，你应该探索数据。

10.1.1  探索一维数据

最简单的情形是，你得到的一个数据集合仅仅是一维数据集。比如，它们可以是每个用户在你的网站上平均每天花费的时间，每个数据科学教程视频的观看次数，或者是你的数据科学图书馆中每本数据科学书的页数。

第一步显然是计算一些总结性统计数据。比如你可能想知道你的数据集中有多少个数据点，最小值是多少，最大值是多少，平均值是多少，或者标准差是多少。

如果你仍不能很好地理解以上步骤，那么下一步最好是绘出直方图，即将你的数据分组成离散的区间（bucket），并对落入每个区间的数据点进行计数：

比如，考虑以下两个数据集：

这两个数据集的均值都接近 0，标准差都接近 58 ，但它们的分布非常不同。

图 10-1 展示了均匀分布：

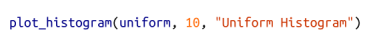
而图 10-2 展示了正态分布：

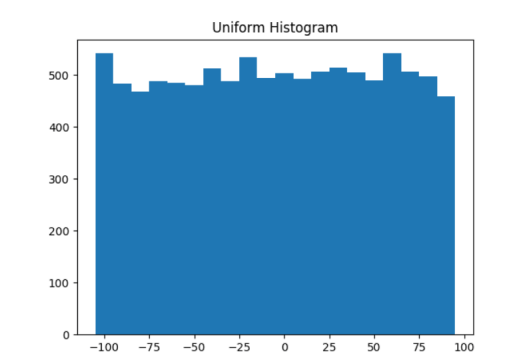
这两种分布有非常不同的最大值和最小值。但是，仅仅知道这一点并不足以理解它们有何差异。

10.1.2  二维数据

现在假设你的数据集是二维的。也许在每天上网时间之外还增加了数据科学工作年限。你当然会希望能从每个维度上单独理解数据，但也许你更希望综合两个维度来考察数据。

比如，考察下面一个伪数据集：

如果你对 ys1 和 ys2 运行 plot_histogram 程序，会得到很相似的直方图（事实上，两个正态分布的均值和标准差都相同）。

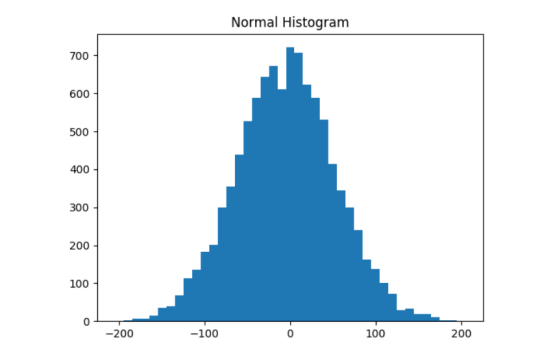
但是在联合分布上，每个都与 xs 有很大差别，如图 10-3 所示：

如果你考察相关性，差异会非常明显：

10.1.3  多维数据

对于多维数据，你可能想了解各个维度之间是如何相关的。一个简单的方法是考察相关矩阵（correlation matrix），矩阵中第 i 行第 j 列的元素表示第 i 维与第 j 维数据的相关性：

一个更为直观的方法（如果维度不太多）是做散点图矩阵（图 10-4），以展示配对散点图。通过命令 plt.subplots() 可以生成子图。我们给出了行数和列数，它返回一个 figure 对象（我们不会用到它）和一个 axes 对象的二维数组（每个都会绘出）：

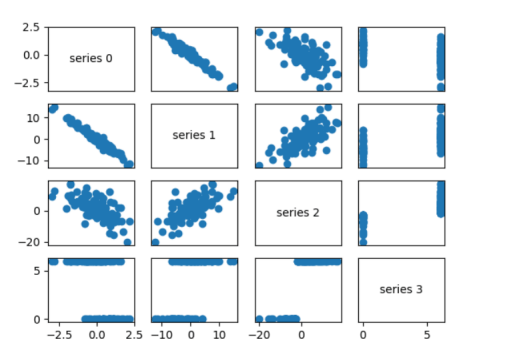
通过这些散点图你会看出，序列 1 与序列 0 的负相关程度很高，序列 2 和序列 1 的正相关程度很高，序列 3 的值仅有 0 和 6，并且 0 对应序列 2 中较小的值，6 对应较大的值。

这是一种能让你查看变量之间大概的相关度的快捷方法（除非你为了查看更加具体的效果而花费数小时调整 matplotlib，这样就不快捷了）。

10.2  使用已命名的元组

表示数据的一种常见方法是使用字典（dicts）：

然而，这并不太理想的原因有几个。这是一种稍微低效的表示（dict 有一些开销），因此，在这个例子中，如果你有很多股票价格，它们会占用更多的内存。但在大多数情况下，这并不重要。

一个更大的问题是，通过字典 key 访问很容易出错。下面的代码运行是没有错误的，只是做了错误的事情：

最后，虽然我们可以对统一字典进行类型注释：

没有任何有用的方法来注释具有许多不同值类型的字典。所以我们也失去了类型提示的价值。作为另一种选择，Python包括一个命名元组（namedtuple）类，它就像一个元组，但有命名：

与常规元组一样，命名元组是不可变的，这意味着一旦创建了它们，你就不能修改其值。虽然这偶尔也会妨碍我们，但大多数情况下这也不失为是一件好事。

你会注意到，我们仍没有解决类型注释问题。我们通过使用类型化变体，即 NamedTuple 解决这个问题 ：

现在编辑器可以帮助你解决，如图 10-5 所示。

10.3  数据集

数据集是 NamedTuple 的一种可变版本。（我之所以说“有点”，是因为 NamedTuple 紧凑地表示它们的数据，而数据集是常规的元组类，只是为你自动生成一些方法。）

该语法与 NamedTuple 非常相似。但是，我们不是从基类继承，而是使用装饰器：

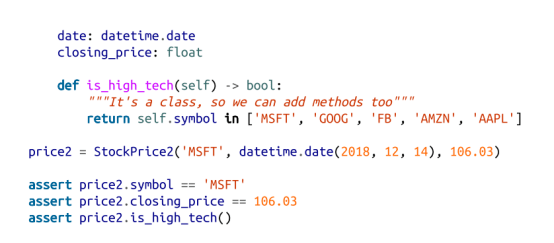
如前所述，最大的区别在于，我们可以修改数据类实例的值：

如果尝试修改 NamedTuple 中的字段的话，我们会得到一个属性错误。

这也使我们容易受到我们期望通过不使用 dict 避免错误的产生的影响：

我们不会使用数据集，但你可能会在野外遇到它们。

10.4  清理与修改

真实世界的数据是有很多问题的。在使用数据之前，你通常需要对它们进行一定的预处理。我们在第 9 章举过这样的例子。我们需要把字符串转化成可以使用的浮点型数据（float）或者整型数据（int）。以前，我们在使用数据之前会这样做：

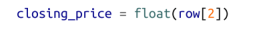
但是，在我们可以测试的函数中进行分析可能不太容易出错：

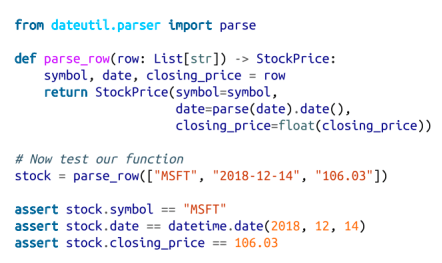
如果数据不好怎么办？一个实际上不代表数字的“浮点数”数值？也许你宁愿得到一个无的东西，也不愿破坏你的程序？

比如，如果我们用逗号分割的股票数据中有不良数据：

我们现在可以在一个单独步骤中读入和解析：

并决定我们想做些什么来处理它们，一般来说，你有三个选择：删除它们；溯源并修复不良数据或缺失数据；什么都不做，自求多福吧。如果数百万行中有一行数据错误，可能可以忽略它。但是，如果你一半的行有错误的数据，这是你需要修复的问题。

下一步要做的是使用“探索数据”或特别调查的技术来检查异常值。例如，你是否注意到股票文件中有一个日期是 3014 年？这不会（一定）给你一个错误，但它很明显是错误的，如果你没有解决它，会得到古怪的结果。真实数据集缺少小数点、额外的零、印刷错误以及你要解决的无数其他问题。（也许这不是你的正式工作，但还有谁会这么做呢？）

10.5  数据处理

数据科学家的核心技能之一就是处理数据。与其说它是一种特定的技术，不如说它是一种通用的方法，所以这里我们只通过一些例子窥其一二。

假设我们需要处理如下股票价格字典：

针对该数据可以提出一些问题。在这个过程中，我们会不断关注做事所使用的模式，并抽象出一些工具以使数据的处理更容易些。

比如，如果我们想知道 AAPL 有史以来的最高收盘价，可以将这个工作分解成具体的步骤：

(1) 将数据限定在包含 AAPL 的行上；

(2) 从每行提取收盘价 closing_price；

(3) 取价格中的最大值 max。

我们可以使用一个列表解析一次性完成这三个步骤：

更一般地，我们也许希望知道数据集中每只股票的最高收盘价。一个方法如下所示。

1. 创建 dict 以跟踪最高价格（我们将使用默认命令，对于缺失值返回负无穷大，因为任何价格都将大于它）。

2. 迭代我们的数据，更新它。

其代码如下：

现在我们可以问一些更复杂的问题，比如在我们的数据集中，单日百分比变动的最大值和最小值分别是什么。百分比变动的公式是 price_today/price_yesterday – 1，这意味着我们需要用某种方式将今天的价格和昨天的价格联系起来。一种方法是按照符号将价格分组，再在每组中：

(1) 按照日期排列价格；

(2) 通过命令 zip 得到配对价格（前一天的，今天的）；

(3) 将配对价格转换为新的“百分比变动”行。

首先，我们按符号将价格分组：

由于价格是元组，所以它们将按字段的顺序排序：首先按符号排序，然后按日期排序，然后按价格排序。这意味着，如果我们有一些价格都有相同的符号，排序将按日期排序（然后按价格排序，这什么都不做，因为我们每个日期只有一个），这就是我们想要的。

我们可以用来计算一系列的日常变化：

然后将它们全部收集起来：

此时，很容易找到最大和最小的一个：

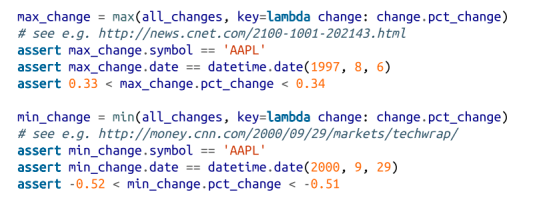
现在我们可以使用这个新的 all_changes 数据集来找出投资科技股的最佳月份。只需按月来查看平均每日变化。

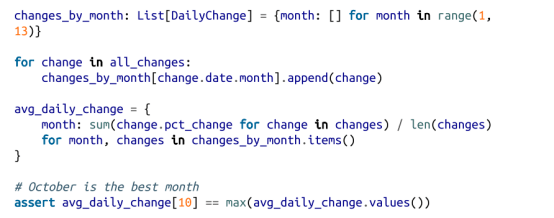
我们将在整本书中进行这类操作，后面不会再明确地说明。

10.6  数据缩放

许多技术对数据量级（scale）敏感。比如，假设你有一个包括数百名数据科学家的身高和体重的数据集，并且需要创建体型大小的聚类（cluster）。

直观上讲，我们用聚类表示相近的点，这意味着我们需要某种点距离的概念。我们知道有欧几里得距离函数 distance，所以自然地，一种方法是将数据对 (height, weight) 视为二维空间中的点。考虑表 10-1 中列出的观测对象。

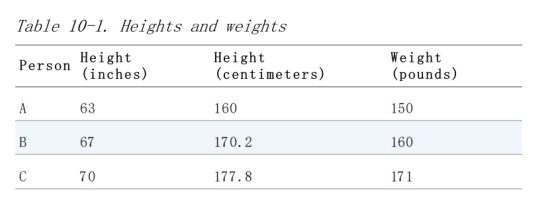
如果我们用英寸作为身高的单位，那么 B 最近的邻居是 A：

但是，如果我们以厘米为单位测量高度，那么 B 的最近邻则是 C：

显然，如果单位变化导致结果发生这样的变化，那肯定是有问题的。因此，如果不同的维度之间不可比较，就需要对数据进行调整（rescale），以使得每个维度的均值为 0，标准差为 1。这种转换有效地摆脱了单位带来的问题，将每个维度转化为“均值的标准差”。

首先，我们需要对每列计算均值和标准差：

然后用结果创建新的数据矩阵：

当然，让我们编写一个测试以符合我们认为应该做的要求：

一如既往地，你需要运用你的判断力。如果你拿到一个由身高和体重组成的巨大的数据集，需要将其过滤为仅由身高在 69.5 英寸至 70.5 英寸之间的人组成。很有可能（取决于你希望回答的问题）剩余的变化仅仅是噪声（noise），但你也许并不希望将其标准差与其他维度的标准差等而视之。

10.7  旁边：tqdm

我们通常会做一些需要很长时间的计算。当你在做这样的工作时，你会想知道你正在取得进展，以及你应该期望等待多久。

其中一种方法是使用 tqdm 库，它会生成自定义的进度条。我们将在书的其余部分中使用它，所以让我们借此机会了解它是如何工作的。

首先，你将需要安装它：

你只需要知道的一些功能。首先，包装在模板中的可迭代文件将产生一个进度条：

产生如下的输出：

特别是，它会显示你完成循环的比例（尽管如果使用生成器则无法完成）、运行时间，以及预期运行时间。

在这种情况下（我们只是调用 range），你可以只使用 tqdm.trange。

你还可以在进度栏运行时设置它的说明。为此，你需要从 with 语句中捕获 tqdm 迭代器：

这会添加如下描述，当一个新质数呗找到时，计算器就更新：

使用 tqdm 有时会使代码出错——有时屏幕重新绘制得不好，有时循环会简单地挂起。如果你不小心将一个 tqdm 循环包裹在另一个 tqdm 循环中，可能会发生奇怪的事情。不过，它的好处通常大于这些缺点，所以每当我们有运行缓慢的计算时，我们就会尝试使用它。

10.8  降维

有时候，数据的“真实”（或有用的）维度与我们具备的数据维度并不相符。比如，考虑图 10-5 中所示的数据。

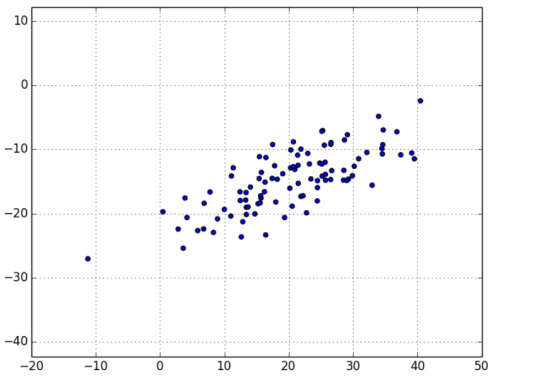
数据的大部分变化看起来像是沿着单个维度分布的，既不与 x 轴对应，也不与 y 轴对应。

当这种情形发生时，我们可以使用一种叫作主成分分析（principal component analysis，PCA）的技术从数据中提取出一个或多个维度，以捕获数据中尽可能多的变化。

首先，我们需要将数据转换成为每个维度均值为零的形式：

（如果不这样做，应用这种技术的结果可能就只是确定数据的均值本身，而非找出数据中的变化。）图 10-7 显示了“去均值”后的示例数据。

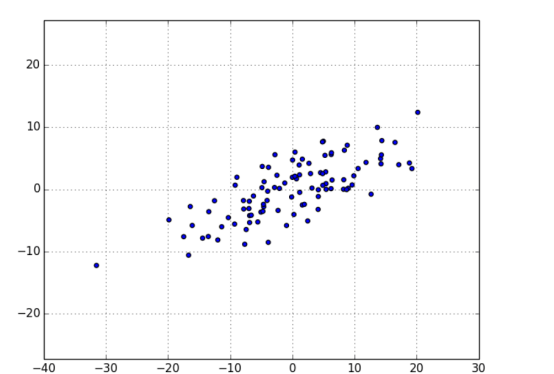
现在，已有一个去均值的矩阵 X，我们想问，最能抓住数据最大变化的方向是什么。

具体来说，给定一个方向 d（一个绝对值为 1 的向量），矩阵的每行 x 在方向 d 的扩展是点积 dot(x, d)。并且如果将每个非零向量 w 的绝对值大小调整为 1，则它们每个都确定了一个方向：

因此，给定一个非零向量 w，我们可以计算我们的数据集在由 w 确定的方向上的方差：

我们可以找出使方差最大的那个方向。只要得到梯度函数，我们就可以通过梯度下降法计算出来：

第一主成分仅是使函数 directional_variance 最大化的方向：

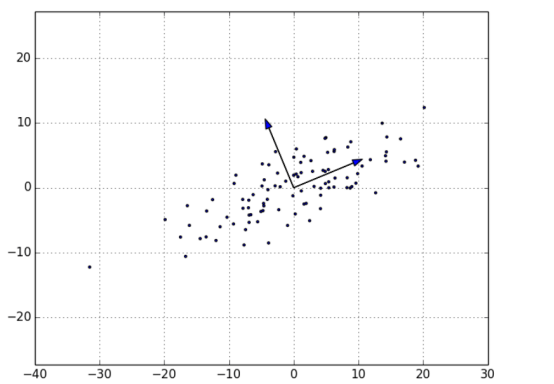
对去均值的数据集，计算结果返回了方向 [0.924, 0.383]，这个方向看起来捕获了数据变动的主要方向轴（图 10-8）。

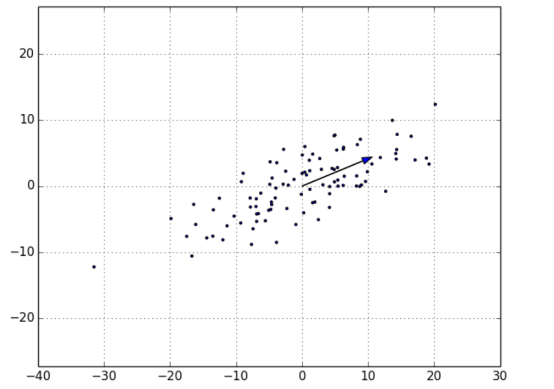
一旦我们找到了第一主成分的方向，我们就可以将数据投影到它上面，以获得投影后的值：

如果要找到更多的成分（component），我们将首先从数据中删除投影：

因为这个例子中的数据集仅仅设定为二维，当移除第一主成分之后，剩下的实际上就是一个一维的成分了（图 10-9）。

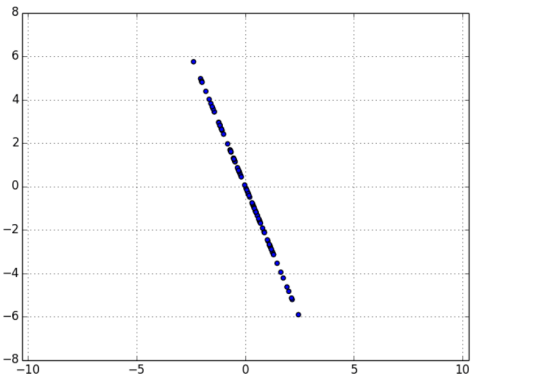
在这点上，我们可以通过对 remove_projection 的结果重复这个过程来找到其他的主成分（图 10-10）。在高维数据集上，我们可以迭代地找到尽可能多的主成分：

然后再将原数据转换为由主成分生成的低维空间中的点：

这种技术很有价值，原因有以下几点。首先，它可以通过清除噪声维度和整合高度相关的维度来帮助我们清理数据。

第二，在获得了数据的低维表示后，我们就可以运用一系列并不太适用于高维数据的技术了。我们可以在本书的很多地方看到运用这种技术的例子。

同时，它既可以帮助你建立更棒的模型，又会使你的模型更难解释。我们很容易理解诸如“工作年限每增加一年，平均工资会增加 1 万美元”这样的结论。但诸如“第三主成分每增加 0.1，平均工资就会增加 1 万美元”这样的结论就很难理解了。

10.9  延伸学习